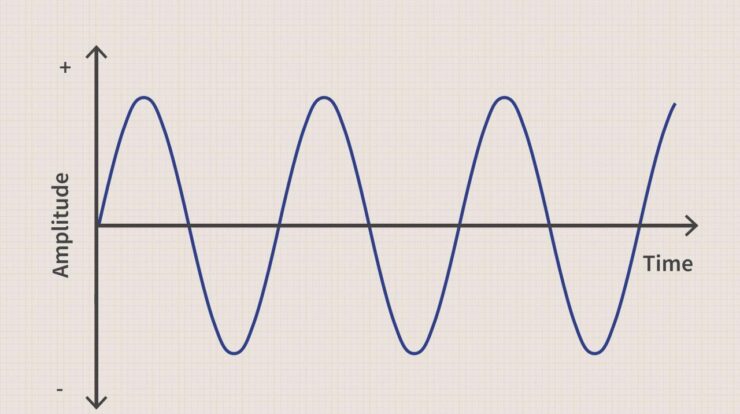
Delving into the world of mathematics, the sine function stands as a cornerstone of trigonometry, playing a crucial role in modeling periodic phenomena and various scientific and engineering applications. In this comprehensive guide, we embark on a journey to unravel the sine meaning, exploring its definition, properties, and diverse uses.
The sine function, denoted as sin(x), is a mathematical function that relates an angle measure to the ratio of the opposite side to the hypotenuse in a right triangle. Its values oscillate between -1 and 1, creating a characteristic wave-like pattern.
Sine Function Basics
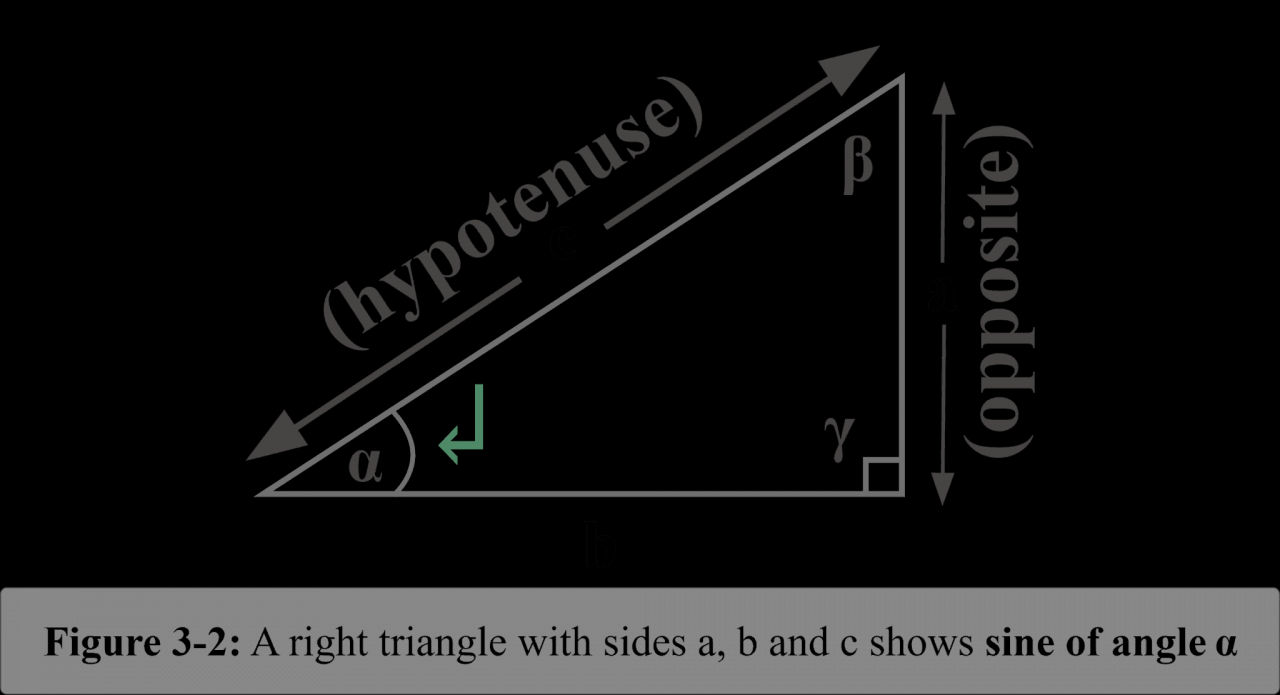
The sine function, denoted as sin(x), is a fundamental trigonometric function that describes the vertical displacement of a point moving along a unit circle as an angle x is measured from the positive x-axis. Mathematically, it is defined as the ratio of the opposite side to the hypotenuse of a right triangle with an angle x.
The domain of the sine function is all real numbers, and its range is between -1 and 1. The graph of the sine function is a smooth, periodic curve that oscillates between its maximum and minimum values.
The sine function is closely related to the unit circle, which is a circle with radius 1 centered at the origin. The coordinates of a point on the unit circle are given by (cos(x), sin(x)), where x is the angle measured from the positive x-axis.
Properties of the Sine Function
- Periodicity:The sine function is periodic with a period of 2π, meaning that it repeats itself every 2π units.
- Symmetry:The sine function is odd, meaning that sin(-x) = -sin(x).
- Behavior at Different Points:
- sin(0) = 0
- sin(π/2) = 1
- sin(π) = 0
- Phase Shift:The sine function can be shifted horizontally by a constant c using the function sin(x
c).
Applications of the Sine Function
- Modeling Periodic Phenomena:The sine function is used to model periodic phenomena such as sound waves, tides, and the motion of a pendulum.
- Engineering and Physics:The sine function is used in fields such as engineering and physics to analyze vibrations, oscillations, and other periodic motion.
- Music:The sine function is used in music to create waveforms and synthesize sounds.
Derivatives and Integrals of the Sine Function, Sine meaning
The derivative of the sine function is the cosine function, and its integral is the negative cosine function.
- Derivative:d/dx sin(x) = cos(x)
- Integral:∫ sin(x) dx = -cos(x) + C
These operations are essential in calculus and have applications in areas such as physics and engineering.
Sine Function in Complex Numbers
The sine function can be extended to complex numbers using the exponential function.
sin(z) = (e^(iz) – e^(-iz)) / (2i)
The complex sine function has properties similar to the real sine function, but it is more versatile and can be used to solve a wider range of problems.
Visual Representation of the Sine Function
| Angle (radians) | sin(x) |
|---|---|
| 0 | 0 |
| π/6 | 1/2 |
| π/4 | √2/2 |
| π/3 | √3/2 |
| π/2 | 1 |
The graph of the sine function is a smooth, periodic curve that oscillates between -1 and 1.
Concluding Remarks: Sine Meaning
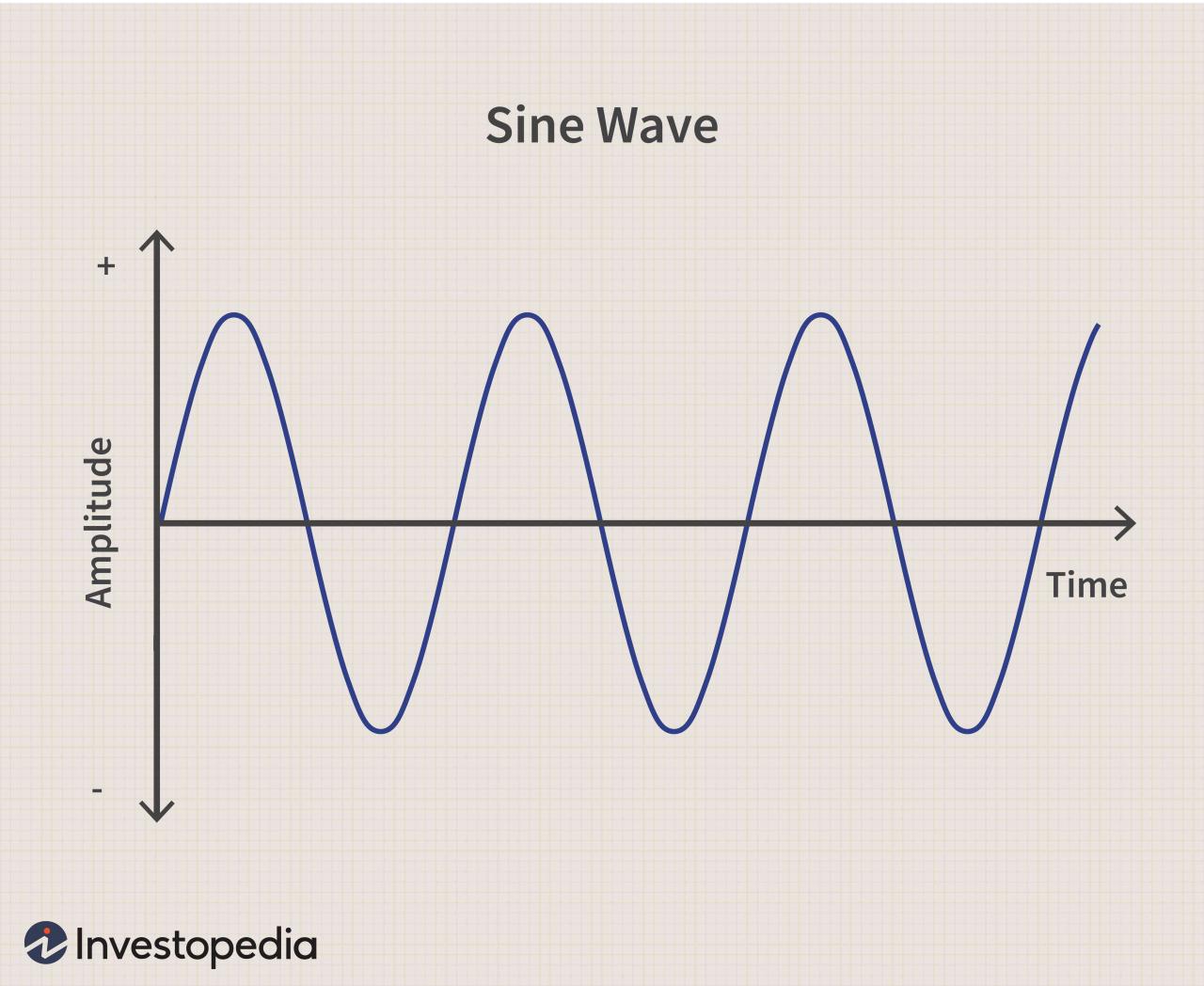
In conclusion, the sine function is a versatile mathematical tool with far-reaching applications across disciplines. Its unique properties and ability to model periodic phenomena make it indispensable in fields such as engineering, physics, and music. Whether used to analyze sound waves, design bridges, or create captivating melodies, the sine function continues to be a cornerstone of scientific and artistic endeavors.
Essential Questionnaire
What is the range of the sine function?
The range of the sine function is [-1, 1].
What is the period of the sine function?
The period of the sine function is 2π.
What is the derivative of the sine function?
The derivative of the sine function is the cosine function: cos(x).





